X CUADRADA COMO PRUEBA DE INDEPENDENCIA DE VARIABLES.

La prueba de independencia Chi-cuadrada, nos permite determinar si existe una relación entre dos variables categóricas.

Cuando la probabilidad de que ocurra un evento aleatorio no está afectada por la ocurrencia de otro evento entonces son variables independientes entre sí, si por el contrario, la ocurrencia del evento aleatorio se ve afectada por la ocurrencia de otra, entonces se trata de variables  dependientes una de otra.

Es necesario resaltar que esta prueba nos indica si existe o no una relación entre las variables, pero no indica el grado o el tipo de relación; es decir, no indica el porcentaje de influencia de una variable sobre la otra o la variable que causa la influencia.

Por ejemplo si  en un colegio se quiere saber si el darle prioridad a tener buenas calificaciones o a ser popular o a participar en deportes es independiente de que el alumno sea niño o niña, esta sería la prueba que podría dar una respuesta, pero no nos va a decir cuáles son las preferencias de las niñas y de los niños, eso lo sabremos al ver que opción es más frecuente en los niño o en las niñas.

Hoy vamos a trabajar con Chi cuadrada como prueba de independencia de variables y la vamos a aplicar a los datos obtenidos sobre los tipos sanguíneos, compararemos para ver si ambas variables (generación y tipo sanguíneo) son o no independientes una de otra, es decir si la frecuencia en los tipos de sangre (por ahora solo en cuanto al sistema A B O) se distribuye independientemente en las 3 generaciones o son dependientes, es decir hay una asociación entre ellas (debido a la herencia)

.

Tenemos entonces las 3 generaciones y 4 tipos sanguíneos.

	A	B	AB	O
Parentales	39	8	6	43
F1	46	5	9	35
F2	48	9	5	50

Hay dos posibles hipótesis:

Ho: Los tipos de sangre se distribuyen de forma independiente en las 3 generaciones.

Ha: Los tipos sanguíneos se distribuyen de manera que es dependiente entre las generaciones.

La prueba de Chi-cuadrado es válida sólo si todas las frecuencias esperadas son mayores a 5, y la muestra fue tomada al azar dentro de la población.

1.        Elaborar una tabla con frecuencias observadas de los tipos de sangre en las 3 generaciones y calcular las sumas parciales de todas las filas y columnas y el gran total (suma de todas las frecuencias)

	A	B	AB	O	Totales
Parentales	39	8	6	43	96
F1	46	5	9	35	95
F2	48	9	5	50	112
Totales	133	22	20	128	303

2.       Calcular las frecuencias esperadas: Asumiendo una distribución independiente para cada una de las combinaciones, se calcula cada frecuencia esperada usando la ecuación siguiente:

                                       f esperada= (total de fila * total de columna)/gran total

	A	B	AB	O	Totales
Parentales					96
F1					95
F2					112
Totales	133	22	20	128	303

3.     Calcular los grados de libertad usando la ecuación:  

grados de libertad =  (m-1)(n-1) 

donde m y n son el número de filas (m) y de columnas (n).

4.       Calcular la chi-cuadrada con la ecuación:

                                                      

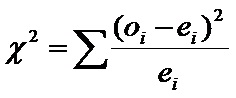
5.       Para este cálculo se construye la siguiente tabla con las frecuencias observadas y esperadas para todas las posibilidades

Cuadrantes con Especie	Frecuencia observada	Frecuencia Esperada (obtenida en el punto 2)
Parental -A
Parental-B
Parental-AB
Parental-O
Σ

En el cuadro resalado en amarillo se obtendrá la sumatoria de esa columna que es el valor de X² calculado y que se compara con el de tablas.

6.       Encuentre el valor crítico en la tabla de Chi-cuadrada de acuerdo a los grados de libertad obtenidos y a un nivel de significancia (p) de 0.05 (5%). (La región crítica es todo valor mayor que el encontrado en la tabla).

7.       Comparar el valor obtenido en la ecuación, con el de la tabla. Si el valor obtenido está en la región crítica (mayor que el encontrado en la tabla) se rechaza la Ho, se acepta entonces la Ha, indicando entonces con un nivel de confianza del 95%,  que hay asociación entre las 2 variables.

                                                            EJERCICIO EXCEL