Desviación Estándar

Para poner esta dispersión de manera cuantificada, se usan varias "medidas de dispersión".
 Para saber como se distribuyen los datos y cuanto se alejan de las medidas centrales, existen diferentes medidas, como por ejemplo:
  • Rango: que es la diferencia entre el valor mínimo y el máximo.
  • Varianza: que muestra la dispersión de los valores alrededor de la media.
S_X^2 = \frac{\sum_{i=1}^n (X_i - \bar{X})^2}{n-1}
  • Desviación estándar: que es la raíz cuadrada de la varianza y a partir de ella se desarrollan diversos métodos de análisis estadísticos,
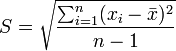
S = \sqrt{\frac{\sum_{i=1}^n (x_i - \bar{x})^2}{n-1}}


Esta formula nos da un número que cuando comparamos entre diferentes poblaciones nos dice cual está más dispersa y cual menos.

Esto es importante porque cuando hacemos un experimento y medimos las desviaciones estándar de nuestros resultados, esperamos que estén en cierta medida agrupados alrededor de la media pues eso nos da confianza de que el experimento es reproducible y de que hemos controlado bien nuestras variables, en caso contrario lo ideal seria aumentar el tamaño de la muestra (mas repeticiones) para disminuir esa dispersión y adicionalmente mejorar el control de las variables.
La interpretación que se da de esta medida parte del hecho de que, al sumar y restar el valor de una desviación estándar al valor de la media, se establece una rango que comprende al 68% de la población, es decir, que si por ejemplo, la media de la estatura de los adultos de una población es 1.75 m, y la desviación estándar es de 12 cm, el 68% de la población mide entre 1.63 y 1.87.
Como ya se menciono, mientras más grande sea la desviación estándar, más dispersos estarán los datos con respecto a la media y por tanto la media será menos representativa de la población.


A continuación está un vínculo, lo que harán ahora es abrirlo y descargarlo,

Calculen la media y desviación estándar, grafiquen los sustratos y la media de la producción de CO2 en una gráfica de columnas y añadan la barra de error personalizada con el valor de la desviación estándar. Una vez hecho esto, vamos a discutir que es lo que representa y como se interpreta.

Comentarios

Publicar un comentario

Entradas populares de este blog

Coeficiente de correlación y de determinación

Imagen
En esta clase vamos a revisar lo que es el  coeficiente de correlación y el de determinación , de hecho ustedes lo han usado cuando en su gráfica ponen una línea de tendencia y ponen lo que hasta ahora conocen como  R2, ese es el coeficiente de determinación  en tanto que su raíz cuadrada, o  sea R (más correctamente r) es el coeficiente de correlación. Una correlación, es simplemente  la relación o dependencia que existe entre las dos variables que intervienen en una  distribución bidimensional . Es decir, la correlación nos indica si los cambios en una de las variables (la independiente) influyen en los cambios de la otra (dependiente). En caso de que suceda, diremos que las variables están correlacionadas o que hay  correlación  entre ellas . Si bien la correlación puede ser exponencial o potencial o lineal, por ahora solo veremos la correlación lineal o de Pearson.   TIPOS DE CORRELACIÓN LINEAL.   1º  Correl...
Leer más

Datos de gráfica a tabla y distribución normal

Imagen
11-12 de septiembre 2018 1.- Trasladar los datos de la gráfica a una tabla de frecuencias absolutas y calcular la frecuencia relativa.         MEDIDAS DE TENDENCIA CENTRAL Son aquellas que   indican alrededor de qué valores se agrupan los datos  observados. Distinguimos: 1. Media aritmética: es el centro de gravedad de la serie de datos y se calcula como .        m- media de la población        x- media de la muestra.             2. Mediana: es el punto medio de una serie ordenada de datos. 3. Moda: es el valor más frecuente de la serie de datos. Cuando  MEDIDAS DE DISPERSION. Cuando ustedes muestren por ejemplo la estatura de todos los alumnos del colegio que tienen entre 16 y 19 años, tendremos estaturas que van desde 1.55 hasta 1.85, dentro de este rango veremos que por lo general los que son más bajitos o más altos son pocos comparados con ...
Leer más

X CUADRADA COMO PRUEBA DE INDEPENDENCIA DE VARIABLES.

Imagen
La prueba de independencia Chi-cuadrada, nos permite determinar si existe una relación entre dos variables  categóricas . Cuando la probabilidad de que ocurra un evento aleatorio no está afectada por la ocurrencia de otro evento entonces son variables independientes entre sí, si por el contrario, la ocurrencia del evento aleatorio se ve afectada por la ocurrencia de otra, entonces se trata de variables  dependientes una de otra. Es necesario resaltar que esta prueba nos indica si existe o no una relación entre las variables, pero  no  indica el grado o el tipo de relación; es decir, no indica el porcentaje de influencia de una variable sobre la otra o la variable que causa la influencia. Por ejemplo si  en un colegio se quiere saber si el darle prioridad a tener  buenas calificaciones  o a  ser popular  o a participar en  deportes  es independiente de que el alumno sea  niño  o  niña,  esta sería ...
Leer más